Characteristics Of A Rational Function

Hotmath

• Home

Rational Functions

A rational part is defined as the quotient of polynomials in which the denominator has a caste of at least $1$ . In other words, in that location must be a variable in the denominator.

The general form of a rational function is

$\frac{p\left(\mathrm{ten}\right)}{q\left(\mathrm{10}\right)}$

, where

$p\left(x\right)$

and

$q\left(\mathrm{10}\right)$

are polynomials and

$q\left(\mathrm{10}\right)\ne 0$

.

Examples:

$y=\frac{3}{\mathrm{ten}},y=\frac{2x+1}{\mathrm{10}+5},y=\frac{\mathrm{ane}}{x^2}$

The parent part of a rational role is $f\left(x\right)=\frac{\mathrm{one}}{x}$ and the graph is a hyperbola .

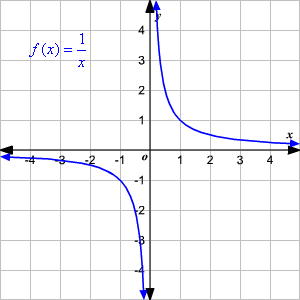
The domain and range is the set of all real numbers except $0$ .

$\begin{array}{l}\text{Domain:}\left\{x|x\ne 0\right\}\\ \text{Range:}\left\{y|y\ne 0\right\}\end{array}$

Excluded value

In a rational function, an excluded value is any $x$ -value that makes the office value $y$ undefined. So, these values should be excluded from the domain of the role.

For example, the excluded value of the function $y=\frac{\mathrm{ii}}{x+3}$ is –3. That is, when $\mathrm{ten}=-3$ , the value of $y$ is undefined.

And then, the domain of this function is set of all real numbers except $-\mathrm{iii}$ .

Asymptotes

An asymptote is a line that the graph of the function approaches, simply never touches. In the parent function $f\left(x\right)=\frac{1}{x}$ , both the $x$ - and $y$ -axes are asymptotes. The graph of the parent function volition get closer and closer to just never touches the asymptotes.

A rational function in the form $y=\frac{a}{x-b}+c$ has a vertical asymptote at the excluded value, or $x=b$ , and a horizontal asymptote at $y=c$ .

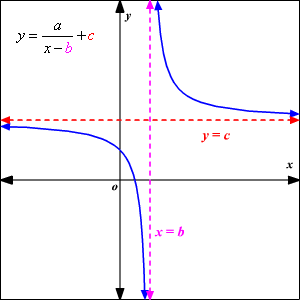
See besides: Graphing Rational Functions

Characteristics Of A Rational Function,

Source: https://www.varsitytutors.com/hotmath/hotmath_help/topics/rational-functions

Posted by: mcintyrerowend.blogspot.com

Share this post